Ενότητες 2 & 3: Δεκαδικοί αριθμοί – Δεκαδικά κλάσματα

Δεκαδικοί αριθμοί – Δεκαδικά κλάσματα

Αξία θέσης ψηφίων στους δεκαδικούς αριθμούς

Η έννοια της στρογγυλοποίησης

Πολλαπλασιασμός δεκαδικών αριθμών

Διαίρεση ακεραίου με ακέραιο με πηλίκο δεκαδικό αριθμό

Γρήγοροι πολλαπλασιασμοί και διαιρέσεις με 10, 100, 1.000

Αναγωγή στη δεκαδική κλασματική μονάδα (1/10, 1/100, 1/1000)

Κλασματικές μονάδες

Iσοδύναμα κλάσματα

 Μετατροπή κλάσματος σε δεκαδικό

 

Τι πράμα είναι το ….κλάσμα ;   

Κλάσμα= μέρος ενός όλου , κομμάτι 

 

Θυμάμαι ότι…………

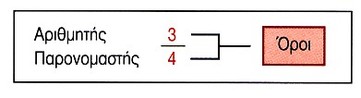
Ένα κλάσμα είναι μέρος ενός "όλου". Υπάρχουν δύο αριθμοί σε κάθε κλάσμα:  O αριθμητής και ο παρονομαστής και  η γραμμή κλάσματος στη μέση.

πχ έχω το κλάσμα  4   

                                                          6

Ο παρονομαστής μου λέει σε πόσα ίσα κομμάτια έχω χωρίσει τον κύκλο (6)

 κι ο αριθμητής πόσα από αυτά έχω χρωματίσει (4)

 

Κλάσμα ή κλασματικός αριθμός είναι ο αριθμός που γίνεται από την κλασματική μονάδα, αν την πάρουμε πολλές φορές.

πΧ Το κλάσμα 4 = 1 + 1 + 1 + 1

                         6    6    6    6     6 

Το κλάσμα με αριθμητή το 1 λέγεται κλασματική μονάδα.

Είναι  δηλαδή το ένα από τα ίσα μέρη στα οποία χωρίζεται η ακέραια μονάδα.

πΧ 1          
       6

                                                          

Περίσσεψε το 1 της πίτσας            Περίσσεψε το 1 της πίτσας                                                2                                                      4

Φάγαμε το 1 της πίτσας                 Φάγαμε τα 3 της πίτσας

                   2                                                     4

 

 

Το κλάσμα εκφράζει το ακριβές πηλίκο μιας διαίρεσης: της διαίρεσης του αριθμητή με τον παρονομαστή του.

3:4 = 3
         4

...και αντίστροφα

Κάνε κλικ και παίξε με τα κλάσματα 

 

skoool™ Kλάσματα

     

•     Οι δεκαδικοί αριθμοί χρησιμοποιούνται όταν θέλουμε να εκφράσουμε με ακρίβεια κάποιες μετρήσεις μεγεθών που είναι μικρότερα  από την ακέραιη μονάδα. Π. χ. 2,4 Ευρώ, 0,23 μ., 2,234 κιλά κ. ά.

       Οι δεκαδικοί αριθμοί αποτελούνται από ένα ακέραιο και ένα δεκαδικό μέρος,  που χωρίζονται με την υποδιαστολή(,)

•      Οι δεκαδικοί γίνονται από την επανάληψη των δεκαδικών μονάδων

πχ

- ο αριθμός 0,3 γίνεται από την επανάληψη της δεκαδικής μονάδας ένα δέκατο 3 φορές       0,1+0,1+0,1=0,3

 - ο αριθμός 0,004 : 0.01+0,01+0,01+0,01

  

·              

       Για να διαβάσουμε ένα δεκαδικό αριθμό διαβάζουμε πρώτα όλο το ακέραιο μέρος του αριθμού, λέμε "και" , και μετά όλο το δεκαδικό μέρος με το όνομα του τελευταίου δεκαδικού ψηφίου.

Π. χ. 3,26 διαβάζεται 3 ακέραιος και 26 εκατοστά

2,135 : διαβάζεται 2 ακέραιος και 135 χιλιοστά

• Όταν ο ακέραιος είναι 0 τότε δε διαβάζεται

Π. χ. 0,345 διαβάζεται 345 χιλιοστά

 

Για να γράψουμε ένα δεκαδικό αριθμό προσέχουμε:

-  Αν ακούμε ότι ο δεκαδικός αριθμός έχει δέκατα, τότε το δεκαδικό μέρος έχει ένα ψηφίο, αν ακούμε εκατοστά έχει δύο και χιλιοστά τρία.

Π. χ. ο αριθμός έξι και πέντε χιλιοστά γράφεται 6,005

ΠΡΟΣΟΧΗ : Η αξία ενός δεκαδικού αριθμού δεν αλλάζει, αν στο τέλος του προσθέσουμε ή αφαιρέσουμε όσα μηδενικά θέλουμε.

Π. χ. 0,3=0,30=0,300 κ. ο. κ.

     

  Κάθε ακέραιο μπορούμε να τον μετατρέψουμε σε δεκαδικό αν βάλουμε στο τέλος του υποδιαστολή και προσθέσουμε όσα μηδενικά θέλουμε(συνήθως βάζουμε δύο)

3= 3,0 ή 3,00 ή 3,000

 

 Μεταφέρω την υποδιαστολή τόσες θέσεις δεξιά, όσα τα μηδενικά Συμπληρώνω με 0. 

3,13 Χ10 = 31,3         3,13 Χ100 = 313   3,13 Χ1000=3130

 Για να διαιρέσω με το 10, 100 1000, μεταφέρω την υποδιαστολή αριστερά, τόσες θέσεις όσα τα 0 . Συμπληρώνω με 0

21,4 : 10 = 2,14          21,4 : 100 = 0,214        21,14 : 1000 = 0, 0214

Κλάσμα και κλασματική μονάδα

Δεκαδικοί αριθμοί

1. Δεκαδικοί αριθμοί και δεκαδικά κλάσματα



2. Δεκαδικά κλάσματα - Δεκαδικοί αριθμοί; πώς γράφω τους 
δεκαδικούς

Στρογγυλοποίηση αριθμών

skoool™ Πολλαπλασιασμός με 10, 100, 1000

Ισοδύναμα κλάσματα - Απλοποίηση κλασμάτων - Ανάγωγα κλάσματα

Εξασκήσου παίζοντας

 

Δραστηριότητες

Κάντε κλικ στους συνδέσμους παρακάτω για να δοκιμάσετε τις ασκήσεις. Σε κάθε άσκηση υπάρχει το κουμπί "Δραστηριότητες" που θα σας οδηγήσει στη σελίδα αυτή

Ανακαλύπτω τα κλάσματα Διάλεξε το σωστό σχήμα - Κλασματικές μονάδες Κάνε τη σωστή αντιστοίχιση - Κλασματικές μονάδες Βρες τον παρονομαστή - Κλασματικές μονάδες Παίρνω ένα μέρος από ένα ποσό - Κλασματικές μονάδες Κάνε τη σωστή αντιστοίχιση - Κλασματικοί αριθμοί Βρες τον αριθμητή & τον παρονομαστή - Κλασματικοί αριθμοί Φτιάξε τα κλάσματα - Κλασματικοί αριθμοί Βρες το κλάσμα ενός ποσού - Κλασματικοί αριθμοί Φτιάξε ισοδύναμα κλάσματα - Ισοδύναμα κλάσματα Γράψε τους αριθμητές και παρονομαστές - Ισοδύναμα κλάσματα Γράψε τους αριθμητές και παρονομαστές - Ισοδύναμα κλάσματα Ποιο κλάσμα είναι ισοδύναμο με ... - Ισοδύναμα κλάσματα

σύντομη ιστορική αναδρομή ..................

το δεκαδικό σύστημα αρίθμησης

 

 Ο άνθρωπος χρειάστηκε 1.000.000 χρόνια για να οδηγηθεί στην αφηρημένη έννοια των αριθμών.

Ο Homo sapiens (300.000 χρόνια πριν) κάνει μια μικρή αρίθμηση με κλαδιά.

  Ο Homo sapiens sapiens (100.000 χρόνια πριν) χρησιμοποιεί κάποιες αριθμητικές λέξεις.

Οι κυνηγοί-τροφοσυλλέκτες (70.000-20.000 χρόνια πριν) καταλάβαιναν την απλή πρόσθεση, τον πολλαπλασιασμό και την αφαίρεση.Το μοίρασμα της     τροφής τους σημαίνει ότι κατανοούσαν τη διαίρεση.

Μέσω της αστρονομίας, της αστρολογίας ή της κοσμολογίας, ο ουρανός άσκησε τη μεγαλύτερη επίδραση στην εξέλιξη των μαθηματικών. 

Σήμερα χρησιμοποιούμε το δεκαδικό σύστημα αρίθμησης. Είναι απλό στη χρήση του: 

Αποτελείται από 10 ψηφία: 0,1,2,3,4,5,6,7,8,9 

Με αυτά μπορώ να φτιάξω απεριόριστους αριθμούς. Γιατί; 

Γιατί η αξία κάθε ψηφίου εξαρτάται από τη θέση του.

 Η αξία κάθε ψηφίου   (από αριστερά προς τα δεξιά) είναι 10 φορές μεγαλύτερη από αυτήν του προηγούμενού του .

ΠΧ  1.111 = (1χ 1.000) + (1χ 100 )+ (1χ10) + 1

Το ίδιο συμβαίνει με τα δέκατα, τα εκατοστά και τα χιλιοστά.

1 δέκατο =10 εκατοστά    1 εκατοστό = 10 χιλιοστά